All Physics Numerical Class 8 ICSE Solutions

PHYSICAL QUANTITIES AND MEASURMENT 

Numericals

Question 1

The density of air is 1.28 g litre^-1. Express it in:

(a) g cm^-3

(b) kg m^-3

Answer

(a) The density of air is 1.28 g litre^-1.

1 litre = 1000 cm³

∴ Density of air in g cm^-3 = ${\displaystyle \frac{\text{1.28}}{\text{1000}}}$

Density of air = 0.00128 g cm^-3

(b) Density of air in kg m^-3 = Density of air in g cm ^-3 x 1000 = 0.00128 x 1000 = 1.28 kg m^-3

∴ Density of air in kg m^-3 = 1.28 kg m^-3.

Question 2

The dimensions of a hall are 10 m x 7 m x 5 m. If the density of air is 1.11 kg m^-3, find the mass of air in the hall.

Answer

Density of air = 1.11 kg m^-3

Volume of hall = 10 m x 7 m x 5 m = 350 m³

Mass = ?

We know,

$$\begin{gathered} \text{Density}={\displaystyle \frac{\text{Mass}}{\text{Volume}}} \\ \text{Mass}=\text{Density}\times \text{Volume} \\ =1.11\times 350 \\ =388.5\text{ kg} \end{gathered}$$

Hence, the mass of air in the hall = 388.5 kg.

Question 3

The density of aluminum is 2.7 g cm^-3. Express it in kg m^-3.

Answer

Density of Aluminum = 2.7 g cm^-3.

Density of aluminum in kg m^-3 = 2.7 x 1000 = 2700 kg m^-3

Hence, Density of aluminum = 2700 kg m^-3.

Question 4

The density of alcohol is 600 kg m^-3. Express it in g cm^-3.

Answer

$$\begin{gathered} {\text{Density of alcohol in g cm}}^{-3}={\displaystyle \frac{{\text{Density of alcohol in kg m}}^{-3}}{\text{1000}}} \\ ={\displaystyle \frac{600}{1000}}=0.6{\text{ g cm}}^{-3} \end{gathered}$$

Hence, Density of Alcohol in g cm^-3 = 0.6 g cm^-3.

Question 5

A piece of zinc of mass 438.6 g has a volume of 86 cm³. Calculate the density of zinc.

Answer

Mass of zinc = 438.6 g

Volume of zinc = 86 cm³

Density of zinc = ?

$$\begin{gathered} \text{Density of Zinc}={\displaystyle \frac{\text{Mass of Zinc}}{\text{Volume of Zinc}}} \\ ={\displaystyle \frac{\text{438.6}}{\text{86}}}=5.1{\text{ g cm}}^{-3} \end{gathered}$$

So, Density of Zinc = 5.1 g cm^-3.

Question 6

A piece of wood of mass 150 g has a volume of 200 cm³. Find the density of wood in

(a) C.G.S. unit

(b) S.I. unit

Answer

Mass of wood = 150 g

Volume of wood = 200 cm³

Density of wood = ?

(a) C.G.S. unit of density is g cm^-3.

$$\begin{gathered} \text{Density of Wood}={\displaystyle \frac{\text{Mass of Wood}}{\text{Volume of Wood}}} \\ ={\displaystyle \frac{\text{150}}{\text{200}}}=0.75{\text{ g cm}}^{-3} \end{gathered}$$

Density of wood = 0.75 g cm^-3.

(b) S.I. unit of density is kg m^-3.

Density of Wood in kg m^-3 = Density of Wood in g cm^-3 x 1000 = 0.75 x 1000 = 750 kg m^-3

So, Density of Wood = 750 kg m^-3.

Question 7

Calculate the volume of wood of mass 6000 kg if the density of wood is 0.8 g cm^-3.

Answer

Density of wood = 0.8 g cm^-3 or 800 kg m^-3

Mass of wood = 6000 kg

Volume of wood = ?

$$\begin{gathered} \text{Density of Wood}={\displaystyle \frac{\text{Mass of Wood}}{\text{Volume of Wood}}} \\ \text{Volume of Wood}={\displaystyle \frac{\text{Mass of wood}}{\text{Density of wood}}} \\ ={\displaystyle \frac{\text{6000}}{\text{800}}}=7.5{\text{ m}}^3 \end{gathered}$$

So, Volume of wood = 7.5 m³.

Question 8

Calculate the density of a solid from the following data:

(a) Mass of solid = 72 g

(b) Initial volume of water in measuring cylinder = 24 mL

(c) Final volume of water when solid is completely immersed in water = 42 mL

Answer

Mass of solid = 72 g

Volume of solid = Final volume of water - Initial volume of water

Volume of solid = 42 - 24 = 18 mL

$$\begin{gathered} \text{Density of Solid}={\displaystyle \frac{\text{Mass of Solid}}{\text{Volume of Solid}}} \\ ={\displaystyle \frac{\text{72}}{\text{18}}}=4 \end{gathered}$$

So, Density of solid = 4.0 g cm^-3.

Question 9

The mass of an empty density bottle is 21.8 g, when filled completely with water it is 41.8 g and when filled completely with liquid it is 40.6 g. Find:

(a) the volume of density bottle.

(b) the relative density of liquid.

Answer

Mass of empty density bottle (M₁) = 21.8 g

Mass of bottle with water (M₂) = 41.8 g

Mass of bottle with liquid (M₃)= 40.6 g

(a) Mass of water in bottle = M₂ - M₁ = 41.8 - 21.8 = 20 g

Density of water is 1 g cm^-3, so volume of density bottle = 20 mL

(b) Mass of liquid in bottle = M₃ - M₁ = 40.6 - 21.8 = 18.8 g

$$\begin{gathered} \text{R.D. of liquid}={\displaystyle \frac{\text{Mass of Liquid}}{\text{Mass of eq. vol. of water}}} \\ ={\displaystyle \frac{\text{18.8}}{\text{20}}}=0.94 \end{gathered}$$

Relative density of liquid = 0.94.

Question 10

From the following observations, calculate the density and relative density of a brine solution.

Mass of empty density bottle = 22 g

Mass of bottle + water = 50 g

Mass of bottle + brine solution = 54 g

Answer

Mass of empty density bottle (M₁) = 22 g

Mass of bottle + water (M₂) = 50 g

Mass of bottle + brine solution (M₃) = 54 g

Mass of water in bottle = M₂ - M₁ = 50 - 22 = 28 g

Density of water is 1 g cm^-3, so volume of density bottle = 28 cm³.

Mass of brine solution in bottle = M₃ - M₁ = 54 - 22 = 32 g

$$\begin{gathered} \text{Density of brine soln.}={\displaystyle \frac{\text{Mass of brine soln.}}{\text{ Vol. of brine soln.}}} \\ ={\displaystyle \frac{\text{32}}{\text{28}}}=1.14{\text{ g cm}}^{-3} \end{gathered}$$

So, density of brine solution = 1.14 g cm^-3.

$$\begin{gathered} \text{R.D. of brine soln.}={\displaystyle \frac{\text{Mass of brine soln.}}{\text{Mass of eq. vol. of water}}} \\ ={\displaystyle \frac{\text{32}}{\text{28}}}=1.14 \end{gathered}$$

So, Relative density of brine solution is 1.14.

Question 11

The mass of an empty density bottle is 30 g, it is 75 g when filled completely with water and 65 g when filled completely with a liquid. Find:

(a) Volume of density bottle,

(b) Density of liquid and

(c) Relative density of liquid.

Answer

Mass of empty density bottle (M₁) = 30 g

Mass of bottle with water (M₂) = 75 g

Mass of bottle with liquid (M₃)= 65 g

(a) Mass of water in bottle = M₂ - M₁ = 75 - 30 = 45 g

Density of water is 1 g cm^-3, so volume of density bottle = 45 mL.

(b) Mass of liquid in bottle = M₃ - M₁ = 65 - 30 = 35 g

$$\begin{gathered} \text{Density of liquid}={\displaystyle \frac{\text{Mass of liquid}}{\text{ Vol. of liquid}}} \\ ={\displaystyle \frac{\text{35}}{\text{45}}}=0.77{\text{ g cm}}^{-3} \end{gathered}$$

So, density of liquid = 0.77 g cm^-3.

(c) $$\begin{gathered} \text{R.D. of liquid}={\displaystyle \frac{\text{Mass of liquid}}{\text{Mass of eq. vol. of water}}} \\ ={\displaystyle \frac{\text{35}}{\text{45}}}=0.77 \end{gathered}$$

So, Relative density of liquid is 0.77

FORCE AND PRESSURE

Numericals

Question 1

Find the moment of force of 20 N about an axis of rotation at a distance of 0.5 m from the force.

Answer

Given:
Force f = 20 N
Distance d = 0.5 m
Moment of force = ?

Moment of force = force f x distance d
= 20 x 0.5
= 10 N m

So, the moment of force = 10 N m.

Question 2

The moment of a force of 25 N about a point is 2.5 N m. Find the perpendicular distance of force from that point.

Answer

Given:
Force f = 25 N
Moment of force = 2.5 N m
Perpendicular distance d = ?

$$\begin{gathered} \text{Moment of force}=\text{force f}\times \text{distance d} \\ \text{Distance d}={\displaystyle \frac{\text{Moment of force}}{\text{Force f}}} \\ ={\displaystyle \frac{\text{2.5}}{\text{25}}} \\ =0.1\text{ m} \end{gathered}$$

So, perpendicular distance of force from the point = 0.1 m or 10 cm.

Question 3

A spanner of length 10 cm is used to unscrew a nut by applying a minimum force of 5.0 N. Calculate the moment of force required.

Answer

Given:
Force f = 5.0 N
Distance d = 10 cm = 0.1 m
Moment of force = ?

Moment of force = force f x distance d
= 5.0 x 0.1
= 0.5 N m

So, Moment of force = 0.5 N m.

Question 4

A wheel of diameter 2 m can be rotated about an axis passing through its centre by a moment of force equal to 2.0 N m. What minimum force must be applied on its rim?

Answer

Given:
Moment of force = 2.0 N m
Diameter = 2 m so radius = 1 m
Therefore perpendicular distance d = radius = 1 m
Force f = ?

$$\begin{gathered} \text{Moment of force}=\text{force f}\times \text{distance d} \\ \text{Force f}={\displaystyle \frac{\text{Moment of force}}{\text{distance d}}} \\ ={\displaystyle \frac{\text{2.0}}{\text{1}}} \\ =2\text{ N} \end{gathered}$$

So, minimum force required is 2 N.

Question 5

A normal force of 200 N acts on an area 0.02 m². Find the pressure in pascal.

Answer

Given:
Force (Thrust) f = 200 N
Area A = 0.02 m²
Pressure = ?

$$\begin{gathered} \text{Pressure}={\displaystyle \frac{\text{Thrust}}{\text{Area}}} \\ ={\displaystyle \frac{\text{200}}{\text{0.02}}} \\ =10000\text{ Pa} \end{gathered}$$

So Pressure = 10000 Pa.

Question 6

Find the thrust required to exert a pressure of 50,000 Pa on an area of 0.05 m².

Answer

Given:
Pressure = 50000 Pa
Area = 0.05 m²
Thrust = ?

Pressure = ${\displaystyle \frac{\text{Thrust}}{\text{Area}}}$

Thrust = Pressure x Area = 50000 x 0.05 = 2500 N

So, Thrust = 2500 N.

Question 7

Find the area of a body which experiences a pressure of 50,000 Pa by a thrust of 100 N.

Answer

Given:
Pressure = 50,000 Pa
Thrust = 100 N
Area = ?

$$\begin{gathered} \text{Pressure}={\displaystyle \frac{\text{Thrust}}{\text{Area}}} \\ \text{Area}={\displaystyle \frac{\text{Thrust}}{\text{Pressure}}} \\ ={\displaystyle \frac{100}{50000}} \\ =0.002{\text{ m}}^2 \end{gathered}$$

So Area of body = 0.002 m² or 2 x 10^-3 m².

Question 8

Calculate the pressure in pascal exerted by a force of 300 N acting normally on an area of 30 cm².

Answer

Given:
Force (Thrust) = 300 N
Area = 30 cm² = ${\displaystyle \frac{30}{10000}}$ = 0.003 m²
Pressure = ?

$$\begin{gathered} \text{Pressure}={\displaystyle \frac{\text{Thrust}}{\text{Area}}} \\ ={\displaystyle \frac{300}{0.003}} \\ =1,00,000\text{ Pa} \end{gathered}$$

So Pressure = 1,00,000 Pa or 10⁵ Pa.

Question 9

How much thrust will be required to exert a pressure of 20,000 Pa on an area of 1 cm²?

Answer

Given:
Pressure = 20000 Pa
Area = 1 cm² = ${\displaystyle \frac{\text{1}}{\text{10000}}}$ = 0.0001 m² or 10^-4 m²
Thrust = ?

Pressure = ${\displaystyle \frac{\text{Thrust}}{\text{Area}}}$
Thrust = Pressure x Area
= 20000 x 10^-4
= 2 N

So Thrust = 2 N.

Question 10

The base of a container measures 15 cm x 20 cm. It is placed on a table top. If the weight of the container is 60 N, what is the pressure exerted by the container on the table top?

Answer

Given:
Weight = Thrust = 60 N
Area = 15 cm x 20 cm = 300 cm² = ${\displaystyle \frac{\text{300}}{\text{10000}}}$ = 0.03 m²
Pressure = ?

$$\begin{gathered} \text{Pressure}={\displaystyle \frac{\text{Thrust}}{\text{Area}}} \\ ={\displaystyle \frac{\text{60}}{\text{0.03}}} \\ =2000\text{ Pa} \end{gathered}$$

So, Pressure = 2000 Pa.

Question 11

Calculate the pressure exerted on a surface of 0.5 m² by a thrust of 100 kgf.

Answer

Given:
Thrust = 100 kgf
Area = 0.5 m²
Pressure = ?

$$\begin{gathered} \text{Pressure}={\displaystyle \frac{\text{Thrust}}{\text{Area}}} \\ ={\displaystyle \frac{\text{100}}{\text{0.5}}} \\ =200{\text{ kgf m}}^{-2} \end{gathered}$$

So Pressure = 200 kgf m^-2.

Question 12

A boy weighing 60 kgf stands on a platform of dimensions 2.5 cm x 0.5 cm. What pressure in pascal does he exert?

Answer

Given:
Thrust = Weight = 60 kgf
1 kgf = 10 N
∴ 60 kgf = 60 x 10 = 600 N
So, Thrust = 600 N

Area = 2.5 cm x 0.5 cm = 1.25 cm² = ${\displaystyle \frac{\text{1.25}}{\text{10000}}}$ = 0.000125 m²
Pressure =?

$$\begin{gathered} \text{Pressure}={\displaystyle \frac{\text{Thrust}}{\text{Area}}} \\ ={\displaystyle \frac{\text{600}}{\text{0.000125}}} \\ =48,00,000\text{ Pa} \end{gathered}$$

So, Pressure = 48,00,000 or 4.8 x 10⁶ Pa.

Question 13

Figure below shows a brick of weight 2 kgf and dimensions 20 cm x 10 cm x 5 cm placed in three different positions on the ground. Find the pressure exerted by the brick in each case.

Answer

First case:

Thrust = Weight = 2 kgf
Area = 20 cm x 10 cm = 200 cm²
Pressure = ?

$$\begin{gathered} \text{Pressure}={\displaystyle \frac{\text{Thrust}}{\text{Area}}} \\ ={\displaystyle \frac{\text{2}}{\text{200}}} \\ =0.01{\text{ kgf cm}}^{-2} \end{gathered}$$

So Pressure exerted by brick in first figure is 0.01 kgf cm^-2.

Second case:

Thrust = Weight = 2 kgf
Area = 5 cm x 10 cm = 50 cm²
Pressure = ?

$$\begin{gathered} \text{Pressure}={\displaystyle \frac{\text{Thrust}}{\text{Area}}} \\ ={\displaystyle \frac{\text{2}}{\text{50}}} \\ =0.04{\text{ kgf cm}}^{-2} \end{gathered}$$

So Pressure exerted by brick in second figure is 0.04 kgf cm^-2.

Third case:

Thrust = Weight = 2 kgf
Area = 20 cm x 5 cm = 100 cm²
Pressure = ?

$$\begin{gathered} \text{Pressure}={\displaystyle \frac{\text{Thrust}}{\text{Area}}} \\ ={\displaystyle \frac{\text{2}}{\text{100}}} \\ =0.02{\text{ kgf cm}}^{-2} \end{gathered}$$

So, Pressure exerted by brick in third figure is 0.02 kgf cm^-2.

ENERGY

Numericals

Question 1

A force of 30 N acts on a body and moves it through a distance of 5 m in the direction of force. Calculate the work done by the force.

Answer

Given:
Force (F) = 30 N
Distance (d) = 5 m
Work done (W) = ?

Work done = Force x distance = 30 N x 5 m = 150 J

So, the work done by the force = 150 J.

Question 2

A man lifts a mass of 20 kg to a height of 2.5 m. Assuming that the force of gravity on 1 kg mass is 10 N, find the work done by the man.

Answer

Given:
Mass (m) = 20 kg
Distance (d) = Height = 2.5 m
Force of gravity on mass of 1 kg = 10 N
Work done (W) = ?

Force (F) = mg = 20 x 10 = 200 N

Work done = Force x distance = 200 x 2.5 = 500 J

So, the work done by the man = 500 J.

Question 3

A body when acted upon by a force of 10 kgf moves to a distance 0.5 m in the direction of force. Find the work done by the force. Take 1 kgf = 10 N.

Answer

Given:
1 kgf = 10 N
10 kgf = 10 x 10 = 100 N
So, Force (F) = 100 N
Distance (d) = 0.5 m
Work done (W) = ?

Work done = Force x distance = 100 x 0.5 = 50 J

So, the work done by the force = 50 J.

Question 4

Two bodies of same masses are placed at height h and 2h. Compare their gravitational potential energy.

Answer

Given:
Mass of first body = Mass of second body = m
Height of first body = h
Height of second body = 2h
g is same for both the bodies.

We know Gravitational potential energy = mgh

Gravitation potential energy of first body (U₁) = mgh
Gravitation potential energy of second body (U₂)= mg2h

On comparing both gravitational potential energy:

${\displaystyle \frac{{\text{U}}_1}{{\text{U}}_2}}={\displaystyle \frac{\text{mgh}}{\text{mg2h}}}={\displaystyle \frac{\text{1}}{\text{2}}}$

So, gravitational potential energy of first body : gravitational potential energy of second body = 1:2.

Question 5

Find the gravitational potential energy of 2.5 kg mass kept at a height of 15 m above the ground. The force of gravity on mass 1 kg is 10 N.

Answer

Given:
Mass (m) = 2.5 kg
Height (h) = 15 m
Force of gravity on mass 1 kg = 10 N

Gravitational potential energy (U) = mgh = 2.5 x 10 x 15 = 375 J

So, gravitational potential energy = 375 J.

Question 6

The gravitational potential energy stored in a box of weight 150 kgf is 1.5 x 10⁴ J. Find the height of the box. Take 1 kgf = 10 N.

Answer

Given:
Gravitational potential energy (U) = 1.5 x 10⁴ J = 15000 J
Weight = 150 kgf = 150 x 10 = 1500 N
height h = ?

U = mgh

15000 = 1500 x h

h = ${\displaystyle \frac{\text{15000}}{\text{1500}}}$

h = 10 m

So height of the box = 10 m.

Question 7

The potential energy of a body of mass 0.5 kg increases by 100 J when it is taken to the top of a tower from the ground. If the force of gravity on 1 kg = 10 N, what is the height of the tower?

Answer

Given:
Potential energy (U) = 100 J
Mass (m) = 0.5 kg
Force of gravity on 1 kg mass = 10 N
height (h) = ?

U = mgh

100 = 0.5 x 10 x h

h = ${\displaystyle \frac{\text{100}}{\text{5}}}$

h = 20 m

So height of the tower = 20 m.

Question 8

A body of mass 60 kg is moving with a speed 50 m s^-1. Find its kinetic energy.

Answer

Given:
Mass (m) = 60 kg
Speed (v) = 50 m s^-1
Kinetic energy = ?

Kinetic energy = ${\displaystyle \frac{\text{1}}{\text{2}}}$ x mv²

= ${\displaystyle \frac{\text{1}}{\text{2}}}$ x 60 x (50)²

= 30 x 2500

= 75000 J or 7.5 x 10⁴ J

So kinetic energy = 7.5 x 10⁴ J.

Question 9

A truck of mass 1000 kg increases its speed from 36 km h^-1 to 72 km h^-1. Find the increase in its kinetic energy.

Answer

Given:

Mass (m) = 1000 kg

1 km h^-1 = ${\displaystyle \frac{\text{5}}{\text{18}}}$ m s^-1

36 km h^-1 = ${\displaystyle \frac{\text{5}}{\text{18}}}$ x 36 = 10 m s^-1

So, initial speed (v₁) = 10 m s^-1

1 km h^-1 = ${\displaystyle \frac{\text{5}}{\text{18}}}$ m s^-1

72 km h^-1 = ${\displaystyle \frac{\text{5}}{\text{18}}}$ x 72 = 20 m s^-1

So, final speed (v₂) = 72 km h^-1 = 20 m s^-1

Increase in its kinetic energy = ?

Increase in kinetic energy = ${\displaystyle \frac{\text{1}}{\text{2}}}$ m[(v₂)² - (v₁)²]

= ${\displaystyle \frac{\text{1}}{\text{2}}}$ x 1000 x [(20)² - (10)²]

= 500 x [400 - 100]

= 500 x 300

= 150000 J or 1.5 x 10⁵ J

So increase in kinetic energy = 1.5 x 10⁵ J.

Question 10

A car is moving with a speed of 15 km h^-1 and another identical car is moving with a speed of 30 km h^-1. Compare their kinetic energy.

Answer

Speed of first car = 15 km h^-1
Speed of second car = 30 km h^-1
Mass of both cars = m

Kinetic energy of first car (K₁) = ${\displaystyle \frac{\text{1}}{\text{2}}}$ x mv²

= ${\displaystyle \frac{\text{1}}{\text{2}}}$ x m x (15)²

= ${\displaystyle \frac{\text{225}}{\text{2}}}$ x m

= 112.5 m J

Kinetic energy of second car (K₂) = ${\displaystyle \frac{\text{1}}{\text{2}}}$ x mv²

= ${\displaystyle \frac{\text{1}}{\text{2}}}$ x m x (30)²

= ${\displaystyle \frac{\text{900}}{\text{2}}}$ x m

= 450 m J

Comparing the kinetic energy we get:

${\displaystyle \frac{{\text{K}}_1}{{\text{K}}_2}}={\displaystyle \frac{\text{112.5 m}}{\text{450 m}}}={\displaystyle \frac{\text{1}}{\text{4}}}$

So Kinetic energy of first car (K₁) : Kinetic energy of second car (K₂) = 1 : 4.

Question 11

A pump raises water by spending 4 x 10⁵ J of energy in 10 s. Find the power of pump.

Answer

Given:
Work done by pump = Energy spent = 4 x 10⁵ J or 400000 J
time = 10 s
Power = ?

Power = ${\displaystyle \frac{\text{Work done}}{\text{time taken}}}$

= ${\displaystyle \frac{\text{400000}}{\text{10}}}$

= 40000 W or 4 x 10⁴ W

So power spent by the pump = 4 x 10⁴ W.

Question 12

It takes 20 s for a girl A to climb up the stairs while girl B takes 15 s for the same job. Compare:

(a) The work done and

(b) The power spent by them.

Answer

(a) Both the girls move the same distance and force is also equal on both. Hence, the work done by both the girls is the same.
∴ Work done by girl A : Work done by girl B = 1 : 1

(b) Power spent = ${\displaystyle \frac{\text{Work done}}{\text{time taken}}}$

We know,

Work done by girl A = Work done by girl B = W

Power spent by girl A (P_A) = ${\displaystyle \frac{\text{W}}{\text{20}}}$

Power spent by girl B (P_B) = ${\displaystyle \frac{\text{W}}{\text{15}}}$

Comparing the power spent by girl A and girl B:

$$\begin{gathered} {\displaystyle \frac{{\text{P}}_{\text{A}}}{{\text{P}}_{\text{B}}}}={\displaystyle \frac{{\displaystyle \frac{\text{W}}{\text{20}}}}{{\displaystyle \frac{\text{W}}{\text{15}}}}} \\ ={\displaystyle \frac{\text{15}}{\text{20}}}={\displaystyle \frac{\text{3}}{\text{4}}} \end{gathered}$$

∴ Power spent by girl A : Power spent by girl B = 3:4

SOUND

Numericals

Question 1

Two waves of the same pitch have amplitudes in the ratio 1:3. What will be the ratio of their:

(i) loudness

(ii) pitch?

Answer

(i) Loudness (L) ∝ [amplitude (a)]²

Ratio of loudness =

${\displaystyle \frac{{\text{L}}_1}{{\text{L}}_2}}={\displaystyle \frac{({\text{a}}_1{)}^2}{({\text{a}}_2{)}^2}}={\displaystyle \frac{(1{)}^2}{(3{)}^2}}={\displaystyle \frac{1}{9}}$

So L₁ : L₂ = 1 : 9.

(ii) Frequency remains the same if the pitch remains unchanged.

${\displaystyle \frac{\text{pitch of 1st wave}}{\text{pitch of 2nd wave}}}={\displaystyle \frac{\text{1}}{\text{1}}}=1:1$

So pitch will be 1 : 1.

Question 2

Two waves have frequencies 256 Hz and 512 Hz, but same amplitude. Compare their:

(i) loudness, and

(ii) pitch.

Answer

(i) Since amplitude of two waves are same so loudness of both the waves will be same.

${\displaystyle \frac{\text{amplitude of 1st wave}}{\text{amplitude of 2nd wave}}}={\displaystyle \frac{\text{1}}{\text{1}}}=1:1$

So, loudness of first wave : loudness of second wave = 1:1.

(ii) Frequency determines the pitch of the sound.

${\displaystyle \frac{\text{frequency of 1st wave}}{\text{frequency of 2nd wave}}}={\displaystyle \frac{\text{256}}{\text{512}}}={\displaystyle \frac{\text{1}}{\text{2}}}=1:2$

So pitch of first wave : pitch of second wave = 1 : 2.

Question 3

Two waves have the same pitch but their amplitudes are in the ratio of 1 : 2. Draw a figure to show the two waves.

Answer

In figure (a) the amplitude of wave A is 2 m and in figure (b) the amplitude of wave B is 4 m. But both the waves have same frequency (pitch).

Ratio of amplitude of wave A to wave B = 2 : 4 = 1 : 2.

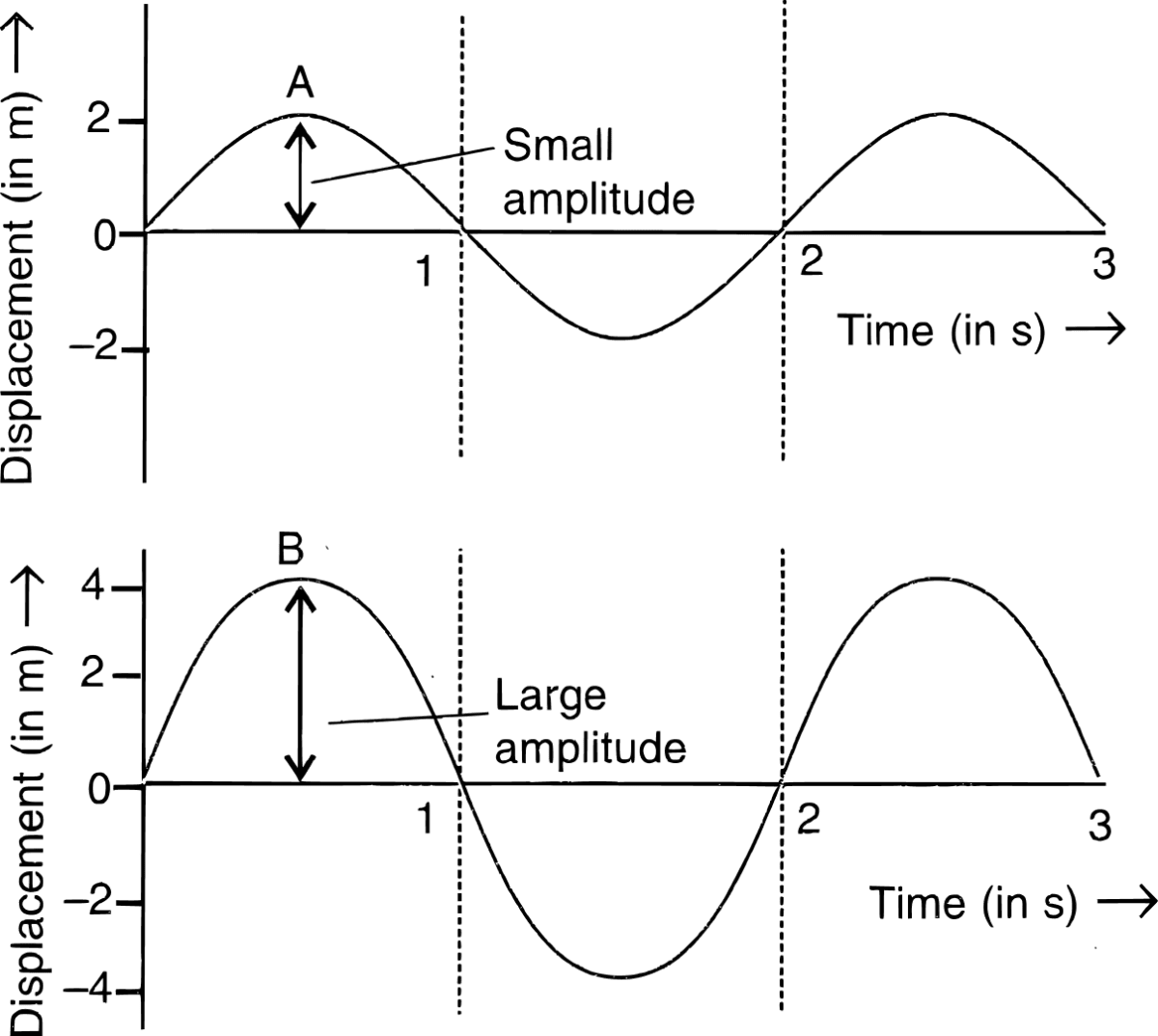
Question 4

Two waves of the same amplitude have frequencies 256 Hz and 512 Hz respectively. Represent the two waves in the graphical form.

Answer

The two waves with frequencies 256 Hz and 512 Hz are represented in graphical form below :

HOUSEHOLD ELECTRICITY

Numericals

Question 1

An electrical appliance is rated as 60 W - 150 V.

(a) What do you understand by this statement?

(b) How much current will flow through the appliance when in use?

Answer

(a) If an electrical appliance is rated as 60 W - 150 V, it means if the appliance is put on a 150 V supply, it will consume 60 W electrical power (i.e., it will consume 60 J of electrical energy in 1 s).

(b) P = 60 W
V = 150 V

We know P = VI

∴ I = ${\displaystyle \frac{\text{P}}{\text{V}}}$ = ${\displaystyle \frac{\text{60}}{\text{150}}}$ = 0.4 A

So, current of 0.4 A will flow through the appliance when in use.

Question 2

An electric iron of power 1.5 kW is used for 30 minutes to press clothes. Calculate the electrical energy consumed in:

(a) kilowatt hour

(b) joule

Answer

Power (P) = 1.5 kW

time (t) = 30 minutes = ${\displaystyle \frac{\text{1}}{\text{2}}}$ hr

(a) Electrical energy consumed in kWh= P x t
= 1.5 x ${\displaystyle \frac{\text{1}}{\text{2}}}$
= 0.75 kWh

So electrical energy consumed in kWh = 0.75 kWh

(b) 1 kWh = 3.6 x 10⁶ J

0.75 kWh = 0.75 x 3.6 x 10⁶

= 2.7 x 10⁶ J

So electrical energy consumed in joule = 2.7 x 10⁶ J.

Question 3

Assuming the electric consumption per day to be 12 kWh and the rate of electricity to be Rs 6.25 per unit, find how much money is to be paid in a month of 30 days?

Answer

Electric energy consumed per day = 12 kWh
Electric energy consumed for 30 days = 12 x 30 = 360 kWh

1 kWh = 1 unit
360 kWh = 360 units
1 unit cost = Rs 6.25
360 units cost = 360 x 6.25 = Rs 2250

So money to be paid for 30 days = Rs 2250.

Question 4

In a premise 5 bulbs each of 100 W, 2 fans each of 60 W, 2 A.Cs each of 1.5 kW are used for 5 h per day. Find:

(a) total power consumed per day,

(b) total power consumed in 30 days,

(c) total electrical energy consumed in 30 days,

(d) the cost of electricity at the rate of Rs 6.25 per unit.

Answer

(a) Power consumed by 5 bulbs = 5 x 100 = 500 W
Power consumed by 2 fans = 2 x 60 = 120 W
Power consumed by 2 A.Cs = 2 x 1.5 = 3 kW or 3 x 1000 = 3000 W
Total power consumed per day = 500 + 120 + 3000 = 3620 W

Total power consumed per day = 3620 W.

(b) Power consumed for 30 days = 30 x 3620 = 108600 W or 108.6 kW

Power consumed for 30 days = 108.6 kW.

(c) Power consumed in 30 days = 108.6 kW
time = 5 h

Electrical energy consumed in 30 days = Power x time
= 108.6 x 5
= 543 kWh

Electrical energy consumed in 30 days = 543 kWh.

(d) Cost of 1 unit = Rs 6.25
Cost of 543 units = 6.25 x 543 = Rs 3393.75

Cost of electricity = Rs 3393.75.